LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS
Aturan Sinus dan Aturan Cosinus merupakan dua aturan yang menghubungkan panjang sisi dan besar sudut dalam segitiga sembarang dengan menggunakan konsep trigonometri. Sesuai dengan namanya, Aturan Sinus melibatkan fungsi sinus, sama halnya dengan Aturan Cosinus. Selain itu, luas segitiga ternyata dapat ditentukan dengan menggunakan bantuan trigonometri, yaitu didasarkan pada besar sudut dan panjang dua sisi yang mengapitnya.
Aturan Sinus
Aturan Sinus (Law of Sines atau Sines Law/Rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan.
Jika diberikan segitiga sembarang
dengan 
Aturan Cosinus
Aturan Cosinus (Law of Cosines atau Cosines Formula/Rule) adalah teorema yang digunakan untuk menentukan panjang sisi depan suatu sudut dengan menggunakan hubungan dua panjang sisi pengapit sudut tersebut dan nilai cosinusnya.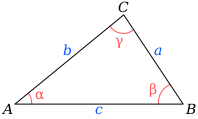
Aturan Luas Segitiga dalam Trigonometri
Misalkan  Dengan demikian, luas
Dengan demikian, luas
Luas segitiga juga dapat dihitung bila diketahui panjang satu sisi dan besar tiga sudutnya.
Untuk memahami lebih dalam mengenai materi ini, berikut disediakan soal dan pembahasannya. Semoga bermanfaat!
Soal Nomor 1
Diketahui
A.
B.
C.
Soal Nomor 2
Pada
A.
B.
Soal Nomor 3
Perhatikan gambar  Perbandingan panjang
Perbandingan panjang
A.
B.
C.
D.
E.
Soal Nomor 4
Pada
A.
B.
C.
Soal Nomor 5
Pada
A.
B.
Soal Nomor 6
Panjang sisi-sisi pada
A.
B.
Soal Nomor 7
Jika panjang sisi-sisi segitiga
A.
B.
C.
Soal Nomor 8
Dalam sebuah lingkaran yang berjari-jari
A.
B.
C.
D.
E.
Nilai 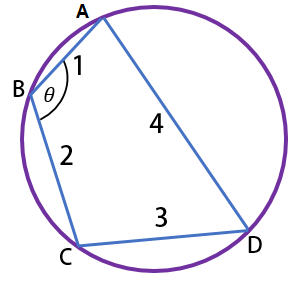 A.
A.
B.
Soal Nomor 10
Perhatikan gambar segi empat 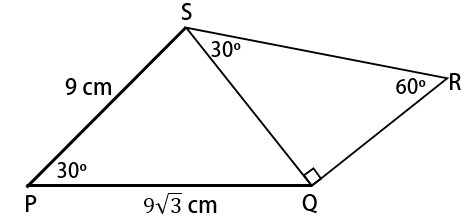 Panjang
Panjang
A.
B.
C.
Soal Nomor 11
Pada segitiga
A.
B.
Soal Nomor 12
Luas segi-
A.
B.
C.
D.
E.
Soal Nomor 13
Jika dalam segitiga
A. segitiga sama sisi
B. segitiga siku-siku
C. segitiga sama kaki
D. segitiga sembarang
E. segitiga tumpul
Soal Nomor 14
Luas segi empat 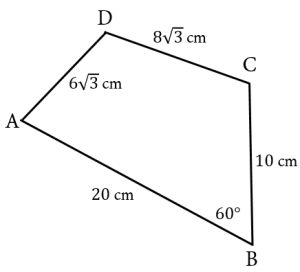 A.
A.
B.
C.
Soal Nomor 15
Sebuah mobil melaju dari tempat
A.
B.
C.
Soal Nomor 16
Keliling suatu segi enam beraturan adalah
A.
B.
C.
Soal Nomor 17
Luas segi-
A.
B.
C.
D.
E.
Soal Nomor 18
Sebuah kapal berlayar dari Pelabuhan A ke Pelabuhan B sejauh
A.
B.
C.
Soal Nomor 19
Sebuah kapal laut berlayar ke arah timur sejauh
A.
B.
C.
Soal Nomor 20
Sukardi dan Lili berdiri di suatu pantai dengan terpisah jarak
A.
B.
Soal Nomor 21
Sebuah mobil melaju dari tempat A sejauh
A.
B.
C.
Soal Nomor 22
Diberikan segitiga
A.
B.
Soal Nomor 23
Diketahui
A.
B.
Soal Nomor 24
Sebuah heksagon (segi enam) diposisikan di dalam segitiga siku-siku seperti gambar berikut. Berapakah luas heksagon tersebut?
Berapakah luas heksagon tersebut?
A.
B.
C.
Soal Nomor 25
Diberikan segitiga 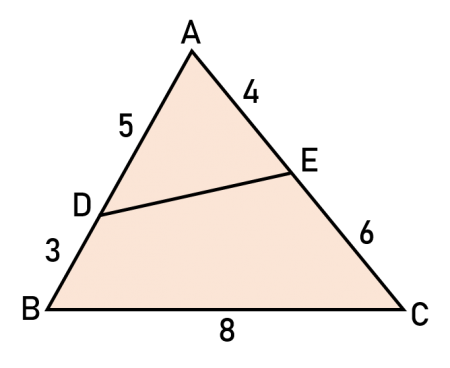 A.
A.
B.
Soal Nomor 26
Pada gambar di bawah, terdapat dua persegi dengan panjang sisi masing-masing 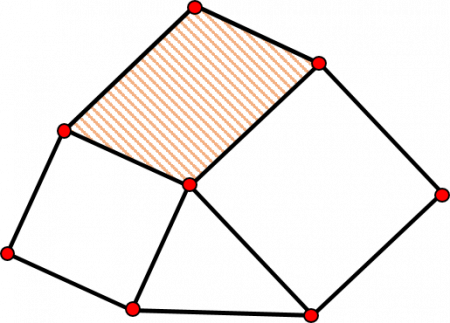 A.
A.
B.
C.
Bagian Uraian
Soal Nomor 1
Pada suatu segitiga
Soal Nomor 2
Diketahui
Soal Nomor 3
Buktikan bahwa dalam segitiga sembarang
Soal Nomor 4
Buktikan bahwa luas segi empat tali busur 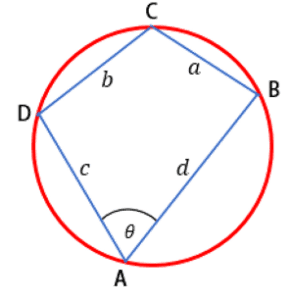
Soal Nomor 5
Pada gambar di bawah, 
Soal Nomor 6
Diketahui
a.
b.

Soal Nomor 7
Buktikan bahwa luas segi empat 
Soal Nomor 8
Pada
Soal Nomor 9
Pada
